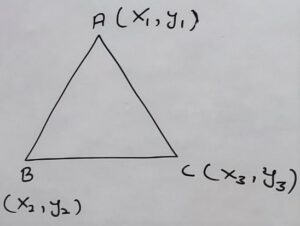
Q.1 Find the area of the triangle whose vertices are :
(i) (2,3),(-1,0),(2,-4)
(ii) (-5,-1),(3,-5),(5,2)
Solution:
(i) (2,3),(-1,0),(2,-4)
Let The co-ordinate of vertices of the triangle are A (2, 3), B (-1, 0), C(2, -4)
x1 = 2 ; y1 = 3
x2 = -1 ; y2 = 0
x3 = 2 ; y3 = -4
Area of Δ ABC = 1/2 [ x1 (y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2) ]
⇒ Area of Δ ABC = 1/2 [ 2 ( 0 + 4 ) + (-1) (-4 – 3) + 2 (3 – 0) ]
⇒ Area of Δ ABC = 1/2 [ 2 ( 4 ) + (-1) (- 7) + 2 (3 ) ]
⇒ Area of Δ ABC = 1/2 [ 8 + 7 + 6 ]
⇒ Area of Δ ABC = 1/2 [21]
⇒ Area of Δ ABC = 21/2 sq. units
(ii) (-5,-1),(3,-5),(5,2)
x1 = -5 ; y1 = -1
x2 = 3 ; y2 = -5
x3 = 5 ; y3 = 2

Area of Δ ABC = 1/2 [ x1 (y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2) ]
⇒ Area of Δ ABC = 1/2 [-5 ( -5 – 2) + 3 (2 + 1) + 5 (-1 + 5) ]
⇒ Area of Δ ABC = 1/2 [-5 (-7) + 3 (3) + 5 (4)]
⇒ Area of Δ ABC = 1/2 [ 35 + 9 + 20 ]
⇒ Area of Δ ABC = 1/2 [ 64 ]
⇒ Area of Δ ABC = 32 sq. units
Q.2 In each of the following find the value ok ‘k’, for which the points are colinear.
(i) (7,-2),(5,1),(3,k)
(ii) (8,1),(k,-4),(2,-5)
Solution:
(i) (7,-2),(5,1),(3,k)
x1 = 7 ; y1 = -2
x2 = 5 ; y2 = 1
x3 = 3 ; y3 = k
Condition for co-linearity
x1 (y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2) = 0
⇒ x1 (y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2) = 0
⇒ 7 (1 – k) + 5(k + 2) + 3(-2 – 1) = 0
⇒ 7 – 7k + 5k + 10 + 3(-3) = 0
⇒ 7 – 7k + 5k + 10 – 9 = 0
⇒ 17 – 2k – 9 = 0
⇒ 8 – 2k = 0
⇒ – 2k = – 8
⇒ k = -8/-2
⇒ k = 4
Q. 3. Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0,-1),(2,1), and (0, 3). Find the ratio of the sides of the triangle whose vertices are (0,-1),(2,1), and (0, 3). Find the ratio of this area of the given triangle.
Solution:
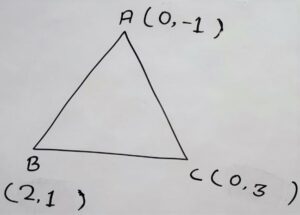
According to diagram
co-ordinates of :
A = (0,-1)
B = (2,1)
C = (0,3)
Mid-point of AB is D
Co-ordinate of D
x = (x1+x2)/2 ; y = (y1+y2)/2 [By mid-point formula]
⇒ x = (0+2)/2 ; y = (-1+1)/2
⇒ x = 1 ; y = (0)/2
⇒ x = 1 ; y = 0
D = (1,0)
Mid-point of BC is E
Co-ordinate of E
x = (x1+x2)/2 ; y = (y1+y2)/2 [By mid-point formula]
⇒ x = (2+0)/2 ; y = (1+3)/2
⇒ x = 2/2 ; y = 4/2
= x = 1 ; y = 2
E = (1,2)
Mid-point of AC is F
Co-ordinate of F
x = (x1+x2)/2 ; y = (y1+y2)/2 [By mid-point formula]
⇒ x = (0+0)/2 ; y = (-1+3)/2
⇒ x = 0/2 ; y = 2/2
⇒ x = 0 ; y = 1
F (0,1)
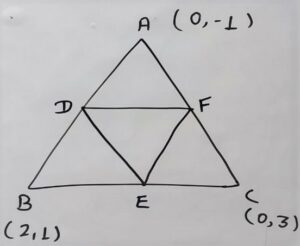
For the area of the triangle DEF
D = (1,0), E = (1,2), F (0,1)
x1 = 1 ; y1 = 0
x2 = 1 ; y2 = 2
x3 = 0 ; y3 = 1
Area of ΔDEF = 1/2 [ x1 (y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2) ]
⇒ Area of ΔDEF = 1/2 [ 1 (2 – 1) + 1 (1 – 0) + 0 (0 – 2) ]
⇒ Area of ΔDEF = 1/2 [ 1 (1) + 1 (1) + 0 (- 2) ]
⇒ Area of ΔDEF = 1/2 [ 1 + 1 + 0 ]
⇒ Area of ΔDEF = 1/2 [ 2]
⇒ Area of ΔDEF = 1 square unit
Here
x1 = 0 ; y1 = -1
x2 = 2 ; y2 = 1
x3 = 0 ; y3 = 3
Area of Δ ABC = 1/2 [ x1 (y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2) ]
⇒ Area of Δ ABC = 1/2 [ 0 (1 – 3) + 2 (3 – {-1}) + 0 (-1 – 1) ]
⇒ Area of Δ ABC = 1/2 [ 0 (-2) + 2 (3 +1) + 0 (-2) ]
⇒ Area of Δ ABC = 1/2 [ 0 + 2 (4) + 0 ]
⇒ Area of Δ ABC = 1/2 [ 0 + 8 + 0 ]
⇒ Area of Δ ABC = 1/2 [ 8 ]
⇒ Area of Δ ABC = 4 square units
For Ratio
Area of Δ DEF÷ Area of Δ ABC = 1÷4
⇒ Area of Δ DEF: Area of Δ ABC = 1:4
Q.4 Find the area of the quadrilateral whose vertices, taken in order, are (-4,-2),(-3,-5),(3,-2), and (2,3).
Solution:
Let Quadrilateral ABCD whose Co-ordinates are
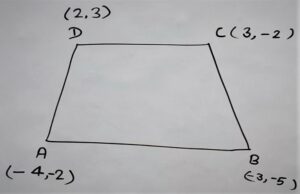
A(-4,-2)
B(-3,-5)
C( 3,-2)
D(2,3)
After joining diagonal AC we get two triangles ΔABC and ΔACD

∴ Area of Quadrilateral ABCD = Area ABC + Area ACD
In Δ ABC
A(-4,-2)
B(-3,-5)
C( 3,-2)
x1 = -4 ; y1 = -2
x2 = -3 ; y2 = -5
x3 = 3 ; y3 = -2
Area of Δ ABC = 1/2 [ x1 (y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2) ]
⇒ Area of Δ ABC = 1/2 [ -4(-5 +2) -3 (-2 + 2) + 3 (-2 + 5) ]
⇒ Area of Δ ABC = 1/2 [ -4(-3) -3 (0) + 3 (3) ]
⇒ Area of Δ ABC = 1/2 [ 12 + 0 + 9 ]
⇒ Area of Δ ABC = 1/2 [ 21 ]
⇒ Area of Δ ABC = 21/2 square units
In Δ ACD
A(-4,-2)
C( 3,-2)
D(2,3)
x1 = -4 ; y1 = -2
x2 = -3 ; y2 = -5
x3 = 2 ; y3 = -3
Area of Δ ACD = 1/2 [ x1 (y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2) ]
⇒ Area of Δ ACD = 1/2 [ -4 (-5 + 3 ) – 3 (-3 + 2) + 2 (-2 + 5) ]
⇒ Area of Δ ACD = 1/2 [ -4 (-2 ) – 3 (-1) + 2 (3) ]
⇒ Area of Δ ACD = 1/2 [ 8 + 3 + 6 ]
⇒ Area of Δ ACD = 1/2 [17]
⇒ Area of Δ ACD = 17/2
Area of Quadrilateral ABCD = Area ABC + Area ACD
⇒ Area of Quadrilateral ABCD = 21/2 + 17/2
⇒ Area of Quadrilateral ABCD = 38/2
⇒ Area of Quadrilateral ABCD = 19 Square units
Q.5 You have studied in Class 9th,(Chapter 9, Example 3), that a median of a triangle divides it into two triangles of equal areas. Verify this result for Δ ABC whose vertices are A(4, -6), B(3,-2), and C(5,2).
Solution:
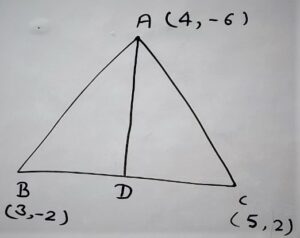
In Δ ABC
From vertex A drawn a median AD on side BC.
Here D is midpoint of B(3,-2) and C(5,2)
By mid-point formula
Co-ordinate of D :
x = (x1+x2)/2 ; y = (y1+y2)/2 [By mid-point formula]
⇒ x = (3+5)/2 ; y = (-2+2)/2
⇒ x = 8/2 ; y = 0/2
⇒ x = 4 ; y = 0
D = (4,0)
Median AD divides the Triangle ABC into two triangles ΔADB and ΔADC
To Prove: Area ΔADB = Area ΔADC
In triangle ADB
A = (4,-6)
D = (4,0)
B = (3,-2)
Area of ΔADB = 1/2 [ x1 (y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2) ]
⇒ Area of ΔADB = 1/2 [ 4 (0 + 2) + 4 (-2 + 6) + 3 (-6 – 0) ]
⇒ Area of ΔADB = 1/2 [ 4 (2) + 4 (4) + 3 (-6 ) ]
⇒ Area of ΔADB = 1/2 [ 8 + 16 – 18 ]
⇒ Area of ΔADB = 1/2 [6]
⇒ Area of ΔADB = 3 square units
In ΔADC
A = (4,-6)
D = (4,0)
C = (5,2)
Area of ΔADC = 1/2 [ x1 (y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2) ]
⇒ Area of ΔADC = 1/2 [ 4(0 – 2) + 4 (2 + 6) + 5 (-6 – 0) ]
⇒ Area of ΔADC = 1/2 [ 4(- 2) + 4 (8) + 5 (-6) ]
⇒ Area of ΔADC = 1/2 [ -8 + 32 -30 ]
⇒ Area of ΔADC = 1/2 [ -38+ 32 ]
⇒ Area of ΔADC = 1/2 [ -6 ]
⇒ Area of ΔADC = -3 (area never be negative)
⇒ Area of ΔADC = 3square units
Hence
Area of ΔABC = Area of ΔACD
