
Q.1 Find the coordinates of the point which divides the join of (-1,7) and (4,-3) in the ratio 2:3.
Solution:
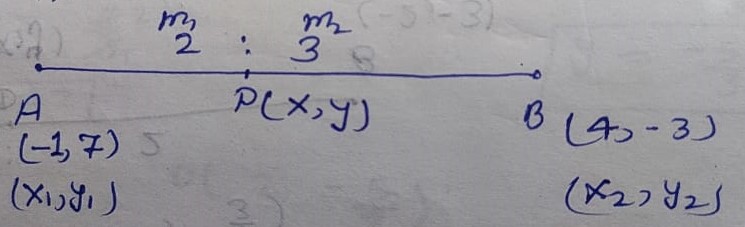
Let A(-1,7) and B(4, -3) and Ratio m1 : m2 = 2 : 3
fig
By Section Formula
Coordinate of P(x, y)
x = (m1x2 + m2x1)/m1+m2 ; y = (m1y2 + m2y1)/m1+m2
⇒ x = (2×4 + 3×-1)/ 2+3 ; y = (2×-3 + 3×7)/2+3
⇒ x = (8 – 3)/5 ; y = (-6 + 21)/5
⇒ x = (5)/5 ; y = (15)/5
⇒ x = 1 ; y = 3
Hence co-ordinate of division point P = (1,3)
Q.2 Find the coordinates of the points of trisection of the line segment joining (4, -1) and (-2,-3).
Solution:

By Section formula
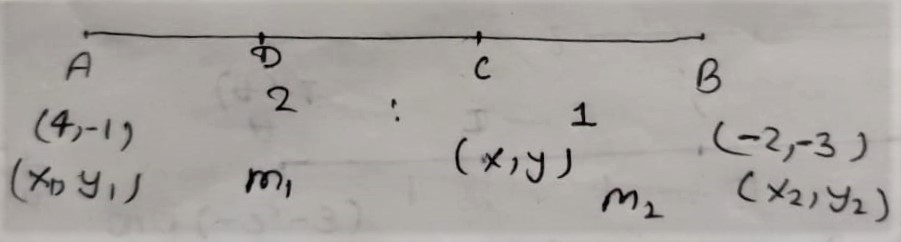
Coordinate of C(x, y)
x = (m1x2 + m2x1)/m1+m2; y = (m1y2 + m2y1)/m1+m2
⇒ x = (2×-2+1×4)/(2+1) ; y = (2×-3 + 1×-1)/(2+1)
⇒ x = (-4 + 4)/3 ; (-6 -1)/3
⇒ x = (0)/3 ; (-7)/3
⇒ x = 0 ; -7/3
C (0, -7/3)
Coordinate of D (x, y)
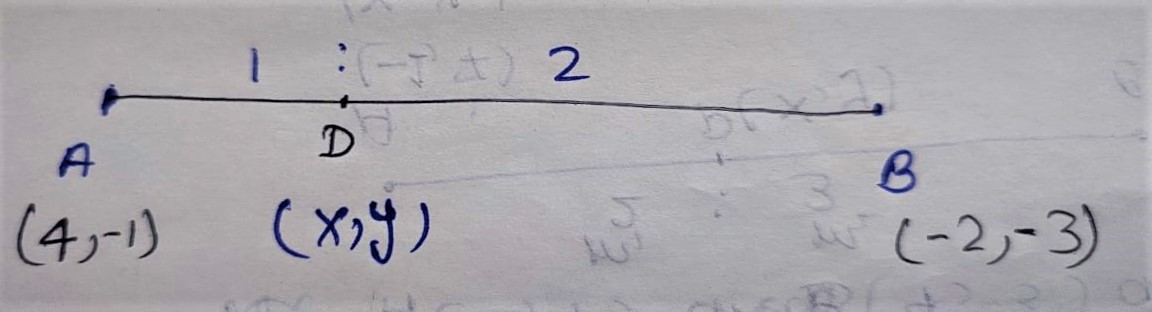
x = (m1x2 + m2x1)/m1+m2; y = (m1y2 + m2y1)/m1+m2
x = (1×-2 + 2×4)/1+2 ; y = (1×-3 + 2×-1)/1+2
⇒ x = (-2 +8)/3 ; y = (-3 -2)/3
⇒ x = 6/3 ; y = (-5)/3
⇒ x = 2 ;
D =(2, -5/3)
Hence co-ordinate of trisection point C (0,-7/3), D (2,-5/3)
Q.4 Find the ratio in which the line segment joining the points (-3,10) and (6, -8) is divided by (-1,6).
Solution:
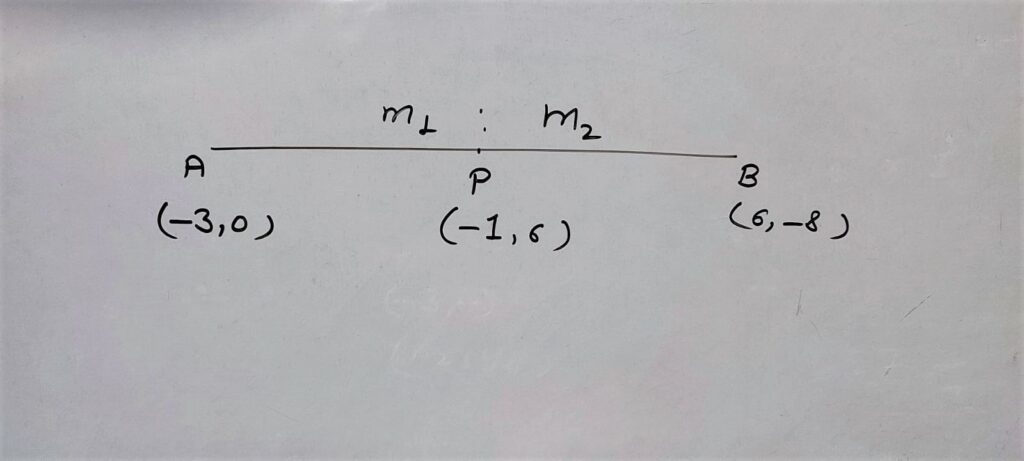
Let Point A(-3,10), and B(6,-8) is divided by P(-1,6) in ration m1: m2
By division/section Formula
x = (m1x2 + m2x1)/m1+m2
⇒ -1 = (m16 + m2×-3)/m1+m2
⇒ -1(m1+m2) = (6m1 -3 m2)
⇒ -m1-m2 = 6m1 -3 m2
⇒ -m1 -6m1 = -3 m2 -m2
⇒ -7m1 = – 4m2
⇒ m1/m2 = -4/-7
⇒ m1/m2 = 4/7
⇒ m1:m2 = 4:7
Hence the ratio = 2 : 7
Note: You can also find the ratio by y coordinate .
Q.5 Find the ration in which the line segment joining A(1, -5) and B(-4, 5) is divided by the x- axis. Also find the coordinates of the point of division.
Solution:
Let the point on x-axis be P(x, 0)
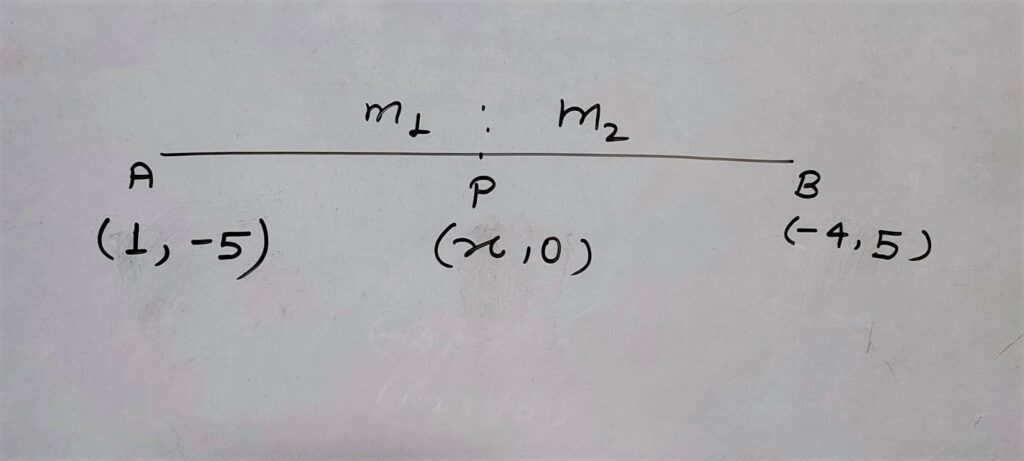
By section formula
y = (m1y2 + m2y1)/m1+m2
⇒ 0 = (m1y2 + m2y1)/m1+m2
⇒ 0 = (m1×5 + m2×-5)/m1+m2
⇒ 0 = (5m1 – 5 m2)/ (m1+m2)
⇒ 0(m1+m2) = 5m1 – 5 m2
⇒ 0 = 5m1 – 5 m2
⇒ 5 m2 = 5m1
⇒ 5/5 = m1/ m2
⇒ 1 : 1 = m1 : m2
∴ division point p is mid point
x = (m1x2 + m2x1)/m1+m2
⇒ x = (1×-4 + 1×1)/1+1
⇒ x = (-4 + 1)/2
⇒ x = -3/2
Hence co-ordinate on x-axis = (-3/2,0)
Q.6 If (1,2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.
Solution:
In parallelogram ABCD Diagonal AC and BD are bisect each other at point O
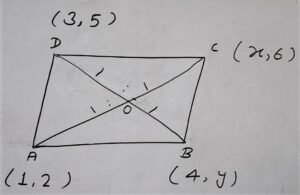
Therefore coordinate of O by A And B = C-ordinate of O by B and D are same.
Now
Coordinate of O by A (1,2) and C (x, 6)
By Mid -point formula
O = (x1+x2/2 , y1+y2/2)
O =(1+x/2 , 2+6/2)
O = (1+x/2 , 8/2)
O = (1+x/2, 4)
Similarly co-ordinate of ) by Diagonal B(4,y) and D (3,5)
O = (x1+x2/2 , y1+y2/2)
O = (4+3/2 , y+5/2 )
O = (7/2 , y+5/2)
By comparing
1+x / 2 = 7/2 ; 4 = y+5/2
⇒ 1+ x = 7 ; 4×2 = y+5
⇒ x = 7-1 ; 8 = y+5
⇒ x = 6 ; 8-5 = y
⇒ x = 6 ; 3 = y
Hence x = 6 and y = 3
Q.7 Find the coordinates of a point A, where AB is the diameter of a circle whose Centre is (2, -3) and B is (1, 4).
Solution:
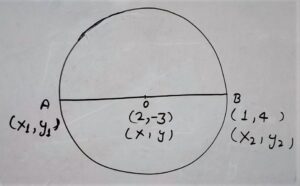
Center O divides Diameter AB in equal Ratio
∴ By mid – point formula
x = (x1+x2)/2 ;
⇒ 2 = (x1+1)/2 ;
⇒ 2×2 = x1+1
⇒ 4 = x1+1
⇒ 4 – 1 = x1
⇒ 3 = x1
y = ( y1+y2)/2
⇒ -3 = (y1+4)/2
⇒ -3×2 = y1+4
⇒ -6 – 4 = y1
⇒ -10 = y1
Hence Co-ordinate of A (3, -5)
Q8. If A and B are (-2, -2) and (2, -4), respectively, find the coordinates of P such that AP = 3/7 AB and P lies on the line segment AB.
Solution:
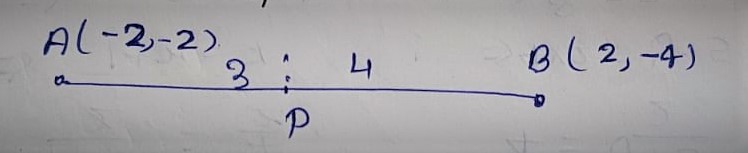
AP = 3/7 AB
⇒ AP/AB = 3/7
PB = AB – AP
PB = 7 – 3 = 4
Let the co-ordinate of P(x, y)
By Section Formula
x = (m1x2 + m2x1)/(m1+m2) ; y = (m1y2 + m2y1)/(m1+m2)
x = (3×2 + 4×-2)/(3+4) ; y = (3×-4 + 4×-2)/(3+4)
x = (6 – 8)/7 ; y = (-12-8)/7
x = -2/7 ; y =-20/7
Hence Co-ordinate of (-2/7 , -20/7)
Q.9 Find the coordinates of the points which divide the line segment joining A(-2, 2) and B(2, 8) into four equal parts.
Solution:
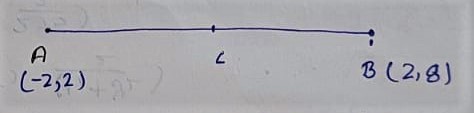
Let mid-point of A(-2, 2) and B(2, 8) is C
C = ( x1+x2 /2 , y1+y2 /2 )
C = ( -2+ 2 /2 , 2+8 /2 )
C = ( 0 /2 , 10 /2 )
C = (0, 5)
Let Mid-point of A(-2,2) and C (0,5) be D
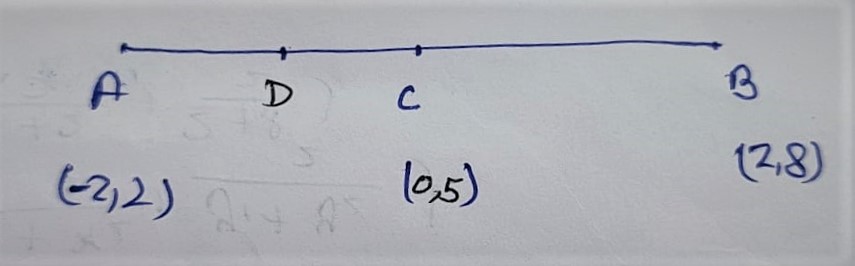
D = ( x1+x2 /2 , y1+y2 /2 )
D = ( -2+0/2 , 2+5/2 )
D = (-2/2 , 7/2)
D = (-1 , 7/2)
Let mid-point of C(0, 5) and B (2, 8) be E
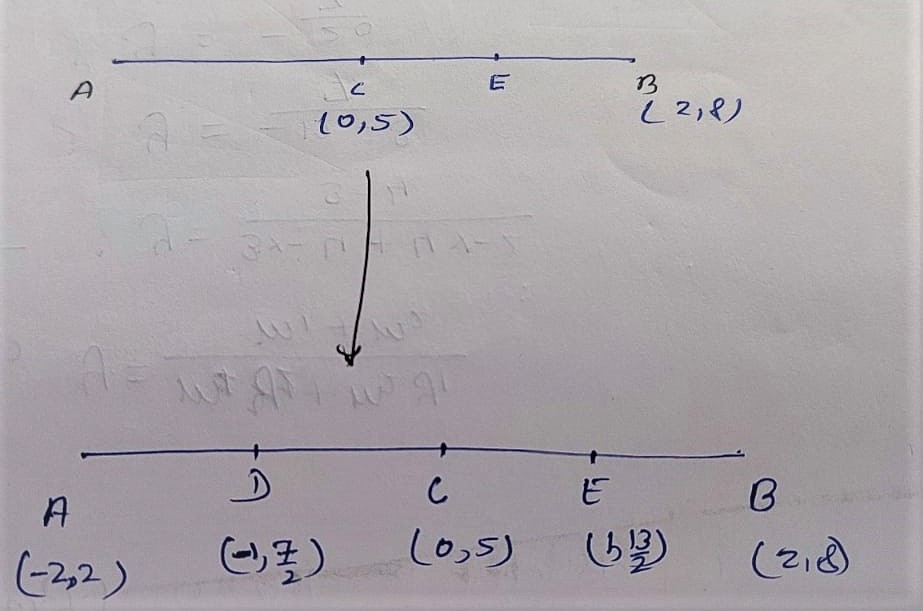
E = ( x1+x2 /2 , y1+y2 /2 )
E = ( 0+2/2 , 5+8/2 )
E = ( 2/2 , 13/2 )
E = (1, 13/2)
Q.10 Find the area of a Rhombus if its vertices are (3, 0),(4, 5),(-1,4) and (-2,-1) taken in order.
Solution:
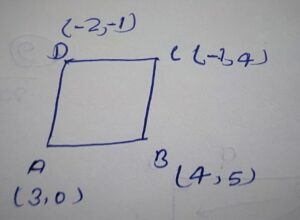
Area of Rhombus = 1/2 (product of diagonals)
⇒ Area of Rhombus = 1/2 ×AC ×BD
By Distance formula
AC = √(x2-x1)² + (y2-y1)²
⇒ A C = √(x2 – x1)² + (y2 – y1)²
⇒ A C = √(-1 – 3)² + (4 – 0)²
⇒ A C = √(-4)² + (4)²
⇒ A C = √16+16
⇒ A C = √32
⇒ A C = 16√2
B D = √(x2-x1)² + (y2-y1)²
⇒ B D = = √(-2 – 4)² + (-1-5)²
⇒ B D = = √(-6)² + (-6)²
⇒ B D = = √36 + 36
⇒ B D = √72
⇒ B D = 6√2
Area of Rhombus = 1/2 ×4√2×6√2
⇒ Area of Rhombus = 24×2/2
⇒ Area of Rhombus = 24 square units.
