Note: All questions Explained By Middle term splitting method/factorisation method.
Q1. Find the roots if the Following quadratic equations by Factorisation:
(i) x² – 3x -10 = 0
Solution:
x² – 3x -10 = 0
⇒ x² – (5 – 2 )x – 10 = 0
⇒ x² – 5x + 2x – 10 = 0
⇒ x(x – 5) + 2(x – 5) = 0
⇒ (x – 5)(x + 2) = 0
x – 5 = 0 ; x + 2 = 0
⇒ x = 5 ; x = – 2
(ii) 2 x² + x – 6 = 0
Solution
2 x² + x – 6 = 0
⇒ 2 x² + (4 – 3)x – 6 = 0
⇒ 2 x² + 4 x – 3 x – 6 = 0
⇒ 2 x ( x + 2 ) – 3 (x + 2) = 0
⇒ (x + 2) (2x – 3) = 0
(2x – 3) = 0 ; (x + 2) = 0
⇒ 2x = 3 ; x = -2
⇒ x = 3/2
Hence x = 3/2, -2
(iii) √2x² + 7x + 5√2 = 0
Solution:
√2x² + (5 + 2 )x + 5√2 = 0
⇒ √2x² + 5x +2x + 5√2 = 0
⇒ x (√2 x + 5) + √2 (√2 x + 5) = 0
⇒ (√2 x + 5)(x + √2 ) = 0
(√2 x + 5) = 0 ; (x + √2 ) = 0
⇒ √2 x = – 5 ; x = – √2
⇒ x = – 5/√2 ;
Hence x = – 5/√2 , – √2
(iv) 2x² – x + 1/8 = 0
Solution:
2x² – x + 1/8 = 0
⇒ (16x² – 8x + 1)/8 = 0
⇒ (16x² – 8x + 1) = 0×8
⇒ 16x² – 8x + 1 = 0
⇒ 16x² -(4 + 4)x + 1 = 0
⇒ 16x² – 4x – 4x + 1 = 0
⇒ 4x(4x – 1) – 1(4x – 1) = 0
⇒ (4x – 1)(4x – 1) = 0
(4x – 1) = 0 ; (4x – 1) = 0
4x = 1 ; 4x = 1
⇒ x = 1/4 ; x = 1/4
⇒ x = 1/4, 1/4
Hence x = 1/4 , 1/4
(v) 100x² – 20x + 1 = 0
Solution:
100x² – (10 + 10)x + 1 = 0
⇒ 100x² – 10x – 10x + 1 = 0
⇒ 10x(10x – 1) + 1(10x – 1) = 0
⇒ (10x – 1)(10x + 1) = 0
10x – 1 = 0 ; 10x + 1 = 0
⇒ 10x = 1 ; 10x = -1
⇒ x = 1/10 ; x = -1/10
Hence x = 1/10 , -1/10
Q.3 Find two numbers whose sum is 27 and product is 182 .
Solution:
Let:
the 1st number be = x
∴ 2nd number = 27 – x
According to condition
Product of two Numbers = 182
x(27 – x) = 182
⇒ 27x – x² = 182
⇒ – x² + 27x – 182 = 0
⇒ -(x² – 27x + 182) = 0
⇒ x² – 27x + 182 = 0
⇒ x² – (14 + 13 )x + 182 = 0
⇒ x² – 14x – 13x + 182 = 0
⇒ x(x – 14) – 13(x – 14) = 0
⇒ (x – 14)(x – 13) = 0
(x – 14) = 0; (x – 13) = 0
⇒ x = 14 ; x = 13
Hence the numbers are 14 and 13
Q4. Find two consecutive positive integers , sum of whose squares is 365.
Solution:
Let two consecutive positive integers are x , x+1
⇒ x² +(x + 1)² = 365
⇒ x² + x² + 2x + 1 = 365
⇒ 2x² + 2x + 1 = 365
⇒ 2x² + 2x + 365 – 1 = 0
⇒ 2x² + 2x + 364 = 0
⇒ 2(x² + x + 182) = 0
⇒ x² + (14 – 13)x – 182 = 0
⇒ x² + 14x – 13x – 182 = 0
⇒ x(x + 14) – 13(x – 14) = 0
⇒ (x + 14)(x – 13) = 0
x + 14 = 0 ; x – 13 = 0
⇒ x = -14 ; x = 13
Hence two consecutive positive integers 13 and 14
Q.5 The altitude of a right triangle is 7 cm less than its base. If the hypotenuse is 13 cm, find the other two sides.
Solution:
Let Base of Right triangle be = x cm.
Altitude = (x -7) cm
Hypotenuse = 13 cm
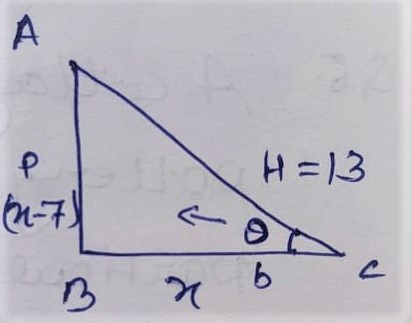
By P.G.T.
(AB)² + (BC)² = (AC)²
P² + b² = H²
⇒ (x -7)² + (x)² = (13)²
⇒ x² – 14x + 49 + x² = 169
⇒ 2x² – 14x + 49 – 169 = 0
⇒ 2x² – 14x – 120 = 0
⇒ 2(x² – 7x – 60) = 0
⇒ x² – 7x – 60 = 0/2
⇒ x² – (12 – 5)x – 60 = 0
⇒ x² – 12x + 5x – 60 = 0
⇒ x(x – 12) + 5(x – 12) = 0
⇒ (x – 12)(x + 5) = 0
x – 12 = 0 ; x + 5 = 0
⇒ x = 12 ; x = -5(not possible)
Hence Base = 12 cm and
Altitude = 12 – 7 = 5 cm
Q.6 A cottage industry produces a certain number of pottery articles in a day. It was observed on a particular day that the cost of production of each article (in rupees) was 3 more than twice the number of articles produced on that day. If the total cost of production on that day was Rs 90, find the number of articles produced and the cost of each article.
Solution:
Let the Number of articles produced in that day = x
Now
The cost of each article om that day = 3 more than twice the numbers of articles
⇒ The cost of each article om that day = 2x + 3
Total cost of production on that day = Rs 90
Number of articles produced × cost of each article = Total cost
⇒ x (2x + 3) = 90
⇒ 2x² + 3x = 90
⇒ 2x² + 3x – 90 = 0
⇒ 2x² + (15 – 12)x – 90 = 0
⇒ 2x² + 15x – 12x – 90 = 0
⇒ x(2x + 15) – 6(2x – 15) = 0
⇒ (2x + 15)(x – 6) = 0
2x + 15 = 0 ; x – 6 = 0
⇒ 2x = -15 ; x = 6
⇒ x = – 15/2 ;
Hence
Number of articles produced on that day = 6
The cost of each article = 2x + 3
⇒ The cost of each article = 2×6 + 3
⇒ The cost of each article = 12 + 3=12 RS
