NCERT Solution Exercise 13.3 Class 10

Q.1 A metallic sphere of radius 4.2 cm is melted and recast into the shape of a cylinder of radius 6 cm. Find the height of the cylinder.

Solution:

Volume of cylinder = Volume of metallic sphere

⇒ πr²H       = 4/3 × πr³

⇒ 6²H         = 4/3 × (4.2)³

⇒ H             = 4/3 × 42/10 × 42/10 × 42/10 × 1/6 × 1/6

⇒ H             = 4× 49 × 14 / 1000

⇒ H             = 2744 / 1000

⇒ H              = 2.744 cm

Hence Height of Cylinder H = 2.744 cm

Q.2 Metallic spheres of radii 6 cm ,8 cm and 10 cm , respectively are melted to form a single solid sphere. Find the radius of the resulting Sphere.

Solution: 

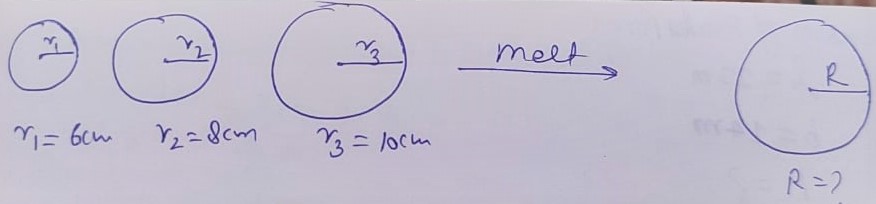
Let

r₁ = 6 cm

r₂ = 8 cm

r₃ = 10 cm

Radius of new solid = R

V₁ + V₂ + V₃  = V

⇒ 4/3 πr³₁ + 4/3 πr³₂+ 4/3 πr³₃  = 4/3 πR³

⇒ 4/3 π [ r³₁ + r³₂+ r³₃ ] = 4/3 πR²

⇒  r³₁ + r³₂+ r³₃  = R³

⇒  6³ + 8³+ 10³  = R³

⇒  216 + 512+ 1000  = R³

⇒  1728  = R³

⇒  ³√1728  = R

⇒  ³√12×12×12×  = R

⇒ 12 = R

Hence Radius of Resulting Sphere R = 12 cm.

Q.3 A 20 m deep well with diameter 7 m is dug and the earth from digging is evenly spread out to form a platform 22 m by 14 m. Find the height of the platform.

Solution:

Diameter of well = 7 cm

r = 7/2

Depth(H) = 20 m

Dimension of platform:

length (l) = 22 m

breadth(b) = 14 m

height (h) =?

Volume of platform = Volume of earth dug out from the well which is in cylindrical shape

⇒ l × b × h = πr²h

⇒ 22 × 14 × h = 22/7 × 7/2 × 7/2 × 20

⇒ h = (11×10×7 )/ (22×14)

⇒ h = 2.5 m

Hence Height of platform = 2.5 m

Q.4 A well of diameter 3 m is dug 14 m deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width 4 m to form an embankment. Find the height of the embankment. 

Solution:

Dimension of Well

Diameter = 3 m

r = 3/2 m

Deep (H) = 14 m

Dimension of Platform(in ring shape):

r = width = 4 m

h =?

Volume of platform = Volume of earth dug out from well

πr²h = πR²H

⇒ r²h = R²H

⇒ 4×4 × h = 3/2 × 3/2 × 14

⇒  h =( 3 × 3 × 14 )/(2×2×4×4)

⇒ h = 63 / 32

⇒ h = 1.96 m

Q.5 A container shaped like a ring circular cylinder having diameter 12 cm and height 15 cm is full of ice-cream. The ice-cream is to be filled into cones of height 12 cm and diameter 6 cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice-cream.

Solution:

Volume of each ice-cream cone = Volume of cone + volume of hemisphere

⇒ Volume of each ice-cream cone = 1/3 πr²h + 2/3 πr³

⇒ Volume of each ice-cream cone = 1/3 × πr² [ h + 2 r ]

⇒ Volume of each ice-cream cone = 1/3 × π 3×3 [ 12 + 2×3 ]

⇒ Volume of each ice-cream cone = 1/3 × π 3×3 [ 12 + 6 ]

⇒ Volume of each ice-cream cone = 3π × 18

Number of Cones = Volume of Container/ Volume of Each Cone

⇒ Number of Cones =  πr²h/ 3π×18

⇒ Number of Cones =  π×6×6×15/ 3π×18

⇒ Number of Cones =  2×5

⇒ Number of Cones =  10

Hence Total Number of Cones Required = 10

Q.6 How many silver coins, 1.75 cm in diameter and of thickness 2 mm must be melted to form a cuboid of dimension 5.5 cm × 10 cm × 3.5 cm.

Given:

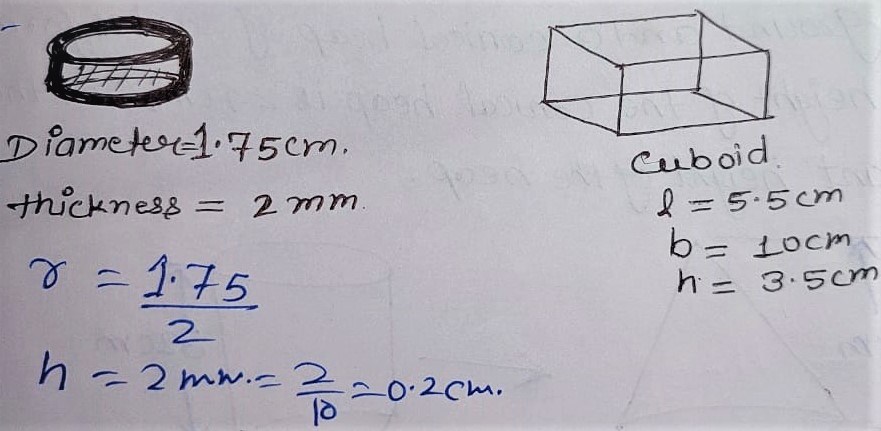
Dimension of silver coin:

Diameter = 1.75 cm

Thickness = 2 mm

r = 1.75/2

h = 2 mm = 2/10 = 0.2 cm

Dimension of cuboid:

l = 5.5 cm

b = 10 cm

h = 3.5 cm

To Find:

Number of coins=?

Solution:

Number of coins = Volume of cuboid / Volume of one coin

⇒ Number of Coins = l × b × h / πr²h

⇒ Number of Coins = (5.5 × 10 × 3.5 )/ (22/7 × 1.75/2 × 1.75/2× 0.2)

⇒ Number of Coins = 10×4×10

⇒ Number of Coins = 400

Hence Total number of coins required to melt = 400

Q.7 A cylindrical bucket, 32 cm high and with radius of base 18 cm, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, find the radius and slant height of the heap.

Solution:

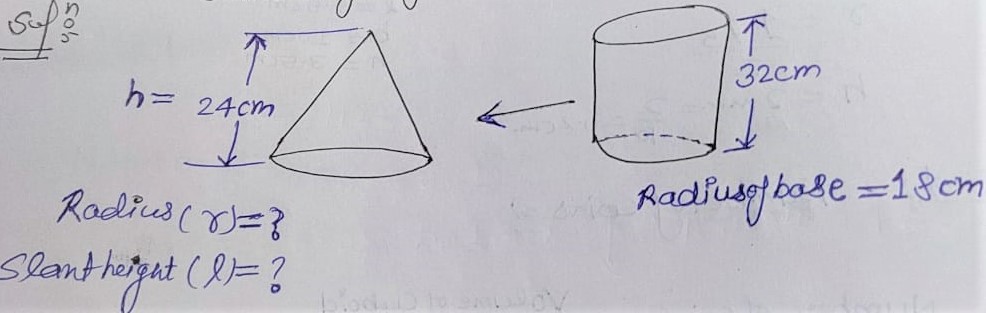
Volume of conical heap = Volume of cylindrical bucket.

⇒ 1/3 πr²h = πr²h

⇒ 1/3 × πr²×24 = π(18)²×32

⇒ 8 r² = 18×18× 32

⇒ r² = 18×18×32/8

⇒ r² = 18×18×4

⇒ r = √18×18×4

⇒ r = 18×2

⇒ r = 36 cm

Slant Height( l )= √r²+h²

⇒ l = √(36²+24²)

⇒ l = √(1296+576)

⇒ l = √(1872)

⇒ l = √2×2×2×2×3×3×13

⇒ l = 2×2×3×√13

⇒ l = 12√13

Hence radius = 36 cm

Slant height = 12√13 cm

Q.8 Water in a canal, 6 m wide and 1.5 m deep , is flowing with a speed of 10 km/hr ,How much area will it irrigate in 30 minutes, if 8 cm of standing water is needed ?

Given:

Speed = 10 km/hr

In 1hour = 60 minutes water flows = 10 km

∴ in 1 minute water will flow = 10/60 km

∴ in 1 minute water will flow = 10/60 ×30 = 5 km=5000 m

Volume of field = volume of water flows in 30 minutes

⇒ Area of field × h = 6×1.5×5000

⇒ Area of field × 8/100 = 6×1.5×5000

⇒ Area of field = 6×1.5×5000 ×100/8

⇒ Area of field = 3×15×2500×5

⇒ Area of field = 45×2500×5

⇒ Area of field = 562500 m²

⇒ Area of field = 56.25 hectares [ 10000 m² = 1 hectares ]

Q.9 A Farmer connects a pipe of internal diameter 20 cm from a canal into a cylindrical tank in her field , which is 10 m in diameter and 2 m deep. If water flows through the pipe at the rate of 3 km/h , in how much time will tank be filled.

Given:

Dimension of pipe:

Diameter = 20 cm

Radius (r) = 20/2 = 10 cm = 10/100 = 1/10 m

Dimension of tank:

Height (h) = deep = 2 m

Diameter = 10 m

r = 10 / 2 = 5 m

Speed of water = 3km/ hr

in 1 hour = 60 minutes water flows = 3 km

∴ in 1 minute water will flow = 3×1000/60 = 50 m

Total time taken to fill the tank = Volume of tank / Volume of water flows through pipe in 1 minute

⇒ Total time taken to fill the tank = πr²h / πr²h

⇒ Total time taken to fill the tank = 5²×2 / 0.1²×50

⇒ Total time taken to fill the tank = 5×5×2 / 0.1×0.1×50

⇒ Total time taken to fill the tank = 5×5×2×10×10/ 1×1×50

⇒ Total time taken to fill the tank = 5×5×2×2

⇒ Total time taken to fill the tank = 100 minutes