Tangent to a Circle : a tangent to a circle is a line which touches or intersect the circle at only one point.

- A tangent to a circle is a special type of secant ,In which both intersect points of secant are coincide.
Theorem 10.1
Prove that ” The tangent at any point of a circle is perpendicular to the radius through the of contact.”
Given:
C ( 0,r)
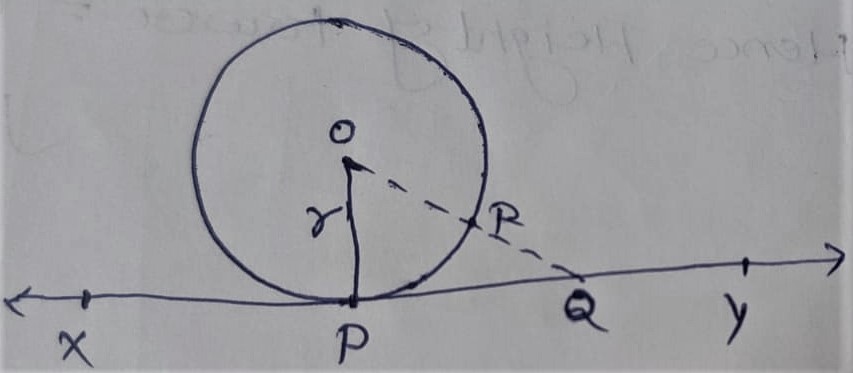
X Y = tangent
P = point of contact
To Prove:
O P ⊥ (perpendicular) on X Y .
Construction:
- Take an another point Q on tangent X Y Except ‘ P ‘
- Joint Q with center O
- O Q intersect the circle at ‘ R ‘
Proof:
In circle:
O P = O R { Radii of same circle } ………….equation(i)
O Q = O R + R Q
O Q > O R { by construction }
∴ O Q > O P { From equation ( i ) }
We can say that all point on tangent are not touches the circle i.e. exterior from the circle only P is touches the circle on tangent which is shortest distance from center O of the circle to the tangent
- Shortest distance is always perpendicular from a point to al line
∴ O P ⊥ ( perpendicular ) on X Y . Hence Proved
Key Point : Radius is always perpendicular on point of contact to the tangent.
Exercise – 10.1
Q. 1. How many tangents can a circle have ?
Answer – Infinitely many tangents
Diagram
Q. 2. Fill in the blanks
( i ) A tangent to a circle intersects it in ……….. point(s)
Ans – One
(ii) A line intersecting a circle in two points is called a …………
Ans – Secant
(iii) A circle can have ………… parallel tangents at the most.
Ans – Two
(iv) The common point of a tangent to a circle and the circle is called ……..
Ans- Point of Contact
Q. 3. A tangent P Q at a point P of a circle of radius 5 cm meets a line through the center O at a point Q so that
O Q = 12cm . Length P Q is :
(A) 12cm
(B) 13cm
(C) 8.5cm
(D) √119cm
Ans- (D)
Explanation:
According to figure

In Δ OPQ
∠P = 90º
By PGT
(OQ)² = (OP)² + (PQ)²
=> (12)² = (5)² + (PQ)²
=> 144 = 25 + (PQ)²
=> 144 – 25 = (PQ)²
=> 119 = (PQ)²
=> √119 = PQ
