Note: In this exercise we will discuss the Areas of Combinations of plane figures .
Q.1. Find the area of the shaded region in figure 12.19 , if PQ = 24 cm , PR = 7 cm and O is the center of the circle.
Given:

P Q = 24 cm
P R = 7 cm
To Find:
Area of shaded Region ..?
Solution:
Angle Subtends with diameter of the circle and any point on the circle always Right angle.
Now in Δ RPQ
P Q = 24 cm
P R = 7 cm
R Q = ?
By P.G.T.
R Q = √(R P)²+(P Q)²
⇒ R Q = √(7)²+(24)²
⇒ R Q = √49+576
⇒ R Q = √625
⇒ R Q = 25
Diameter of circle = 25 cm
Area of shaded region = Area of semicircle – Area of triangle RPQ
⇒ Area of shaded region = πr²/2 – 1/2 × base × height
⇒ Area of shaded region = 1/2×22/7×25/2×25/2 – 1/2 ×24× 7
⇒ Area of shaded region = (11×25×25)/7×4 – 84
⇒ Area of shaded region = (6875)/28 – 84
⇒ Area of shaded region = (6875 – 2352)/28
⇒ Area of shaded region = (4523)/28 cm²
Q.2. Find the area of the shaded region in fig 12.20 , if radii of the two concentric circles with center o are 7 cm and 14 cm respectively and ∠AOC = 40°

Solution:
Two Concentric Circles
r1 = 14 cm
r2 = 7 cm
θ = 40°
Area of shaded Region = Area of sector with r1 =14cm – Area of sector with r2 = 7cm
⇒ Area of shaded Region = θπr1²/360° – θπr2²/360°
⇒ Area of shaded Region = θπ/360°( r1² – r2² )
⇒ Area of shaded Region = 40/360 × 22/7(14² – 7² )
⇒ Area of shaded Region = 40/360 × 22/7(196 – 49 )
⇒ Area of shaded Region = 40/360 × 22/7 × 147
⇒ Area of shaded Region = 154/7 cm²
Q.3. Find the area of the shaded region in figure 12.21, if ABCD is a square of side 14 cm and APD and BPC are semi-circles.
Given:
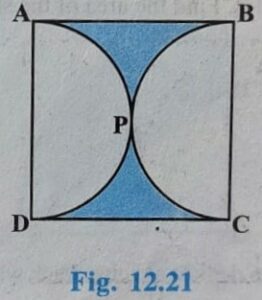
In Square ABCD:
side = 14 cm
APD and BPC are semicircles
To Find:
Area of Shaded Region = ?
Solutions:
Diameter of semicircle APD = Diameter of semicircle BPC = side of Square =14 cm
Radius = 14/2 = 7 cm
Area of Shaded Region = Area of Square ABCD – 2 × Area of Semicircle
⇒ Area of Shaded Region = side × side – 2 × ( πr²/2 )
⇒ Area of Shaded Region = 14 × 14 – 2 × 22/7 × 7 × 7 )
⇒ Area of Shaded Region = 196 – 154
⇒ Area of Shaded Region = 42 cm²
Q.4. Find the area if the shaded region in figure 12.22, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as center.
Given:

In Figure
C ( O , r )
r = 6 cm.
Δ OAB is a equilateral triangle
Side = 12 cm
To Find:
Area of Shaded region =?
Solution:
Here ΔOAB is a equilateral triangle
∴ Each interior angles are also equal = 60°
θ = 60°
Area of Shaded Region = Area of major sector + Area of equilateral triangle ABC
⇒ Area of Shaded Region = (360 – θ)/360 × π r² + √3/4 × a²
⇒ Area of Shaded Region = (360 – 60)/360 ×22/7 × 6² + √3/4 × 12²
⇒ Area of Shaded Region = (300)/360 ×22/7 × 6 × 6 + √3/4 × 12 × 12
⇒ Area of Shaded Region = (5×22×6)/7 + 36√3
⇒ Area of Shaded Region = (660/7 + 36√3) cm²
Q.5. From each corner of a square of side 4 cm a quadrant of circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in figure 12.23. Find the area of the remaining portion of the square.
Given:

Quadrilateral ABCD is a square ,
4 quadrant with radius r= 1 cm
Inside a circle with Diameter = 2 cm.
Radius of circle = 2/2 = 1cm
To Find:
Area of Remaining Portion = ?
Solution:
Area of Remaining portion = Area of Square – 4×Area of Quadrant – Area if circle
⇒ Area of Remaining portion = side ×side – 4×1/4 ×π r² – π r²
⇒ Area of Remaining portion = 4×4 – π r² – π r²
⇒ Area of Remaining portion = 16 – 2 π r²
⇒ Area of Remaining portion = 16 – 2 × 22/7 × 1×1
⇒ Area of Remaining portion = 16 – 44/7
⇒ Area of Remaining portion = (112 – 44)/7
⇒ Area of Remaining portion = 68/7 cm²
Q.6. In a circular table cover of radius 32 cm , a design is formed leaving an equilateral triangle ABC in the middle as shown in figure 12.24. Find the area of the design.
Given:

r = 32 cm
In design ABC is a equilateral triangle
To Find:
Area of Design = ?
Solution:
θ = Angle on center of the circle = 360/3 =120°
Area of Remaining portion of the Design = 3× Area of minor segment
⇒ Area of Remaining portion of the Design = 3× [ θπ/360 – sin(θ/2) cos(θ/2) ] r²
⇒ Area of Remaining portion of the Design = 3× [ 120/360 ×22/7 – sin(60/2) cos( 60/2) ] 32²
⇒ Area of Remaining portion of the Design = 3× [ 22/21 – sin30 cos30 ] 32²
⇒ Area of Remaining portion of the Design = 3× [ 22/21 – √3/4 ] 32²
⇒ Area of Remaining portion of the Design = [ (3× 22×32×32)/21 – 3×32×32×√3/4 ]
⇒ Area of Remaining portion of the Design = [ 22528/7 – 768√3 ]cm²
Q.7. In Figure 12.25 , ABCD is a square of side 14 cm . with Centers A, B, C and D, Four circles are drawn such that each circle touch externally two of the remaining three circles. Find the area if the shaded region.
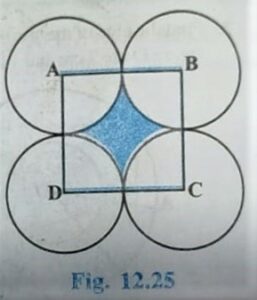
Solution:
ABCD is a square
∠A =∠B =∠C =∠D = 90°
Each circle has Radius = 14/2 = 7 cm
Area of Shaded Region = Area of Square – 4×Area of sector
⇒ Area of Shaded Region = side ×side – 4×θ×πr²/360
⇒ Area of Shaded Region = 14×14 – 4×(90/360)×(22/7)×7×7
⇒ Area of Shaded Region = 196 – 22×7
⇒ Area of Shaded Region = 196 – 154
⇒ Area of Shaded Region = 42 cm²
Q.8. Figure 12.26 depicts a racing track whose left and right ends are semicircular. The distance between the two inner parallel line segments is 60 m and they are each 106 m long . If the track is 10 m wide. Find:
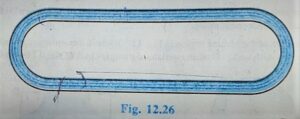
(i) the distance around the track along its inner edge
(ii)the area of the track.
Solution:
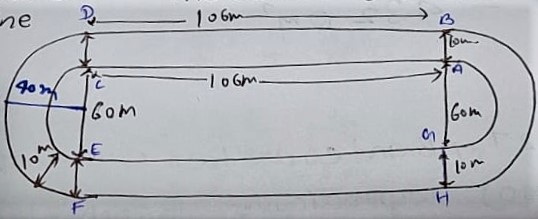
The distance around the track along its inner edge = Length A B + E G + 2×πr
⇒ The distance around the track along its inner edge = 106 + 106 + 2×22/7×60/2
⇒ The distance around the track along its inner edge = 212 + 1320/7
⇒ The distance around the track along its inner edge = 2804/7 m
(ii) The area of the track = Area Rectangle ABCD + Area Rectangle EFGH + 2×[Area of semicircle with r= 40m – Area of semicircle with r=30m]
⇒ The area of the track = l×b + l×b + 2 [ πr1²/2 – πr2²/2 ]
⇒ The area of the track = 106×10 + 106×10 + 2 [ πr1²/2 – πr2²/2 ]
⇒ The area of the track = 1060 + 1060 + 2 ×1/2[ πr1² – πr2² ]
⇒ The area of the track = 2120 + π[ r1² – r2² ]
⇒ The area of the track = 2120 + π[ 40² – 30² ]
⇒ The area of the track = 2120 + π[ 1600 – 900 ]
⇒ The area of the track = 2120 + 22/7 ×700
⇒ The area of the track = 2120 + 2200
⇒ The area of the track = 2120 + 22/7 ×700
⇒ The area of the track = 4320 m²
Q.9. In Figure 12.27, A B and C D are two diameters of a circle (with center o) Perpendicular to each other and O D is the diameter of the smaller circle. If O A = 7cm, Find the area of the shaded region.

Solution:
O A = O B = O D = O C [ Radii of same circle ]
⇒ r = O A = 7 cm.
θ = 90°
Diameter of smaller circle = 7 cm
Radius r1 = 7/2
Area of Shaded Region = Area of Smaller Circle + 2×Area of Minor Segment
⇒ Area of Shaded Region = πr1² + 2×[θπ/360 – sin(θ/2)cos(θ/2)] r²
⇒ Area of Shaded Region = 22/7 × 7/2 ×7/2 + 2×[90/360 ×22/7 – sin(90/2)cos(90/2)] 7²
⇒ Area of Shaded Region = 77/2 + 2×[ 11/14 – sin(45)cos(45)] 7²
⇒ Area of Shaded Region = 77/2 + 2×[ 11/14 – 1/√2×1/√2 ] 7²
⇒ Area of Shaded Region = 77/2 + 2×[ 11/14 – 1/2 ] 7²
⇒ Area of Shaded Region = 77/2 + 2×[(11-7)/14 ] 7²
⇒ Area of Shaded Region = 77/2 + 2×[4/14 ] 7²
⇒ Area of Shaded Region = 77/2 + 28
⇒ Area of Shaded Region = (77+56)/2
⇒ Area of Shaded Region = 133/2
⇒ Area of Shaded Region = 66.5 cm²
Q.10. The area of an equilateral triangle ABC is 17320.5 cm². With each vertex of the triangle as center , a circle is drawn with radius equal to half the length of the side of the triangle (see figure 12.28). Find the area of the shaded region. ( use π = 3.14 and √3 = 1.73205)
Given:
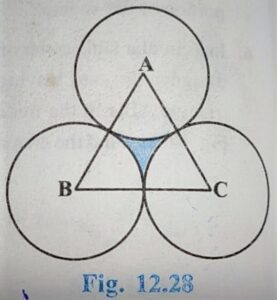
Area of equilateral triangle = 17320.5 cm²
Radius of all circles are equal
To Find:
Area of shaded region = ?
Solution:
Area of equilateral triangle = 17320.5 cm²
⇒ √3/4 a² = 17320.5
⇒ a² = 17320.5×4/√3
⇒ a² = 17320.5×4/1.73205
⇒ a² = 40000
⇒ a = √40000
⇒ a = 200
Each side of Triangle = 200 cm
Radii of each circle = side of equilateral triangle /2
⇒ Radii of each circle = 200/2
⇒ Radii of each circle (r)= 100
Each interior angle of equilateral triangle = 60°
Area of Shaded Region = Area of equilateral triangle ABC – 3×Area of sector
⇒ Area of Shaded Region = 17320.5 – 3×θπr²/360
⇒ Area of Shaded Region = 17320.5 – 3×(60/360)×3.14×100×100
⇒ Area of Shaded Region = 17320.5 – 15700
⇒ Area of Shaded Region = 1620.5 cm²
Hence shaded region = 1620.5 cm²
Q.11. On a square handkerchief, nine circular designs each of radius 7 cm are made (see figure 12.29).Find the area of the remaining portion of the handkerchief.
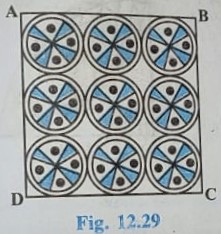
Solution:
Radius of each circular Design = 7 cm
Diameter = 2×7=14 cm
Side of square = 42 cm
The area of the remaining portion of the handkerchief = Area of Square – 9×πr²
⇒ The area of the remaining portion of the handkerchief = Side ×Side – 9×πr²
⇒ The area of the remaining portion of the handkerchief = 42×42 – 9×22/7 ×7²
⇒ The area of the remaining portion of the handkerchief = 1764 – 9×154
⇒ The area of the remaining portion of the handkerchief = 1764 – 1386
⇒ The area of the remaining portion of the handkerchief = 378 cm²
Q.12. In figure 12.30, OACB is a quadrant of a circle with center O and radius 3.5 cm , If O D = 2 cm. Find the area of the (i) Quadrant OACB (ii) Shaded Region

Solution:
Radius of Quadrant r = 3.5 cm
O D = 2 cm
(i) The area of quadrant OACB = πr²/4
⇒ The area of quadrant OACB = 1/4 × 22/7 × 3.5 × 3.5
⇒ The area of quadrant OACB = 77/8 cm²
(ii) Area of the shaded region = Area of quadrant – Area of Δ BOD
⇒ Area of the shaded region = 77/8 – 1/2 × b× h
⇒ Area of the shaded region = 77/8 – 1/2 × 3.5× 2
⇒ Area of the shaded region = 77/8 – 7/2
⇒ Area of the shaded region = 49/8 cm²
Q.13. In figure 12.31, a square OABC is inscribed in a quadrant OPBQ. If O A = 20 cm, Find the area of the Shaded region ( use π = 3.14 )
Solution:
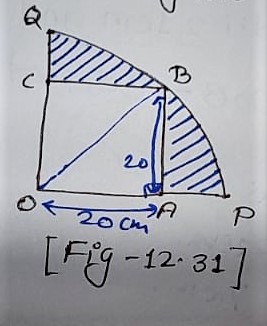
OABC = Square
Side = 20 cm
In triangle OAB
∠A = 90°
By P.G.T.
OB² = OA² + AB²
⇒ OB² = (20)² + (20)²
⇒ OB² = 400 + 400
⇒ OB² = 800
⇒ OB = √800
⇒ OB = 20√2 cm
Radius of quadrant =20√2 cm
Area of Shaded Region = Area of quadrant OPBQ – Area of square OABC
⇒ Area of Shaded Region = (1/4)×πr² – side × side
⇒ Area of Shaded Region = 1/4 ×3.14×20√2×20√2 – 20×20
⇒ Area of Shaded Region = 1/4 ×3.14×20×20×2 – 400
⇒ Area of Shaded Region = 628 – 400
⇒ Area of Shaded Region = 228 cm²
Q. 14. A B and C D are respectively arcs of two concentric circles of radii 21 cm and 7 cm and center O ( see figure 12.32 )If ∠AOB = 30°, Find the area if the shaded region.

Solution:
θ = 30°
O B = 21 cm
O C = 7 cm
Area of Shaded Region = Area of Sector with r1 = 21cm – Area of sector r1= 7cm
⇒ Area of Shaded Region = θπ r1²/360 – θπ r2²/360
⇒ Area of Shaded Region = θπ/360 ( r1² – r2² )
⇒ Area of Shaded Region = 30×22/360×7( 21² – 7² )
⇒ Area of Shaded Region = 30×22/360×7[( 21+7 )(21-7)]
⇒ Area of Shaded Region = 11/6×7[( 28 )(14)]
⇒ Area of Shaded Region = 11×2×14/3
⇒ Area of Shaded Region = (22×14)/3
⇒ Area of Shaded Region = 308/3 cm²
Q.15. In Figure 12.33 ,ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of shaded region.

Given:
ABC is a quadrant
a semicircle with Diameter BC
To Find:
Area of Shaded Region =?
Solution:
In triangle ABC
∠A = 90°
By P.G.T.
BC =√(AB)²+(AC)²
⇒ BC =√(14)²+(14)²
⇒ BC =√(196+196)
⇒ BC =√2×196
⇒ BC =14√2
Diameter = 14√2
r = 14√2/2
⇒r = 7√2
Area of Shaded Region = Area of Semicircle – Area of minor segment
⇒ Area of Shaded Region = πr²/2 – [ θπ/360 – sin(θ/2)cos(θ/2)]
⇒ Area of Shaded Region = πr²/2 – [ 90π/360 – sin(90/2)cos(90/2)]
⇒ Area of Shaded Region = 1/2 × 22/7×(7√2)² – [ 22/7×4 – 1/√2 × 1/√2 ](14)²
⇒ Area of Shaded Region = 11×7×√2×√2 – [ 11/7×2 – 1/2 ](14)²
⇒ Area of Shaded Region = 77×2 – [ 11/7×2 – 1/2 ](14)²
⇒ Area of Shaded Region = 154 – [ 11/14 – 1/2 ](14)²
⇒ Area of Shaded Region = 154 – [ (4)/14 ](14)²
⇒ Area of Shaded Region = 154 – 56
⇒ Area of Shaded Region = 98 cm²
Q.16. Calculate the are of the designed region in Figure 12.34 common between the two quadrants of circles of radius 8 cm each.
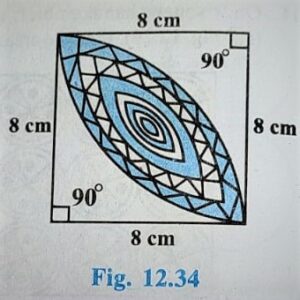
Solution:
Area of Design = 2× [ Area of Minor Segment ]
Area of Design = 2×[θπ/360 – sin(θ/2)cos(θ/2)] r²
Area of Design = 2×[90π/360 – sin(90/2)cos(90/2)] 8²
⇒ Area of Design = 2×[π/4 – sin45cos45]8²
⇒ Area of Design = 2×[22/7 ×1/4 – 1/√2 × 1/√2]8²
⇒ Area of Design = 2×[11/14 – 1/2]8²
⇒ Area of Design = 2×[(11 – 4)/14 ]8²
⇒ Area of Design = 2×[4/14 ]8²
⇒ Area of Design = 256/7 cm²
